正規乱数の生成
中心極限定理
中心極限定理とは下記のとおり。
赤本からの引用です。
母集団分布が何であっても、確率変数の和
の確率分布の形は
が大なるときには大略正規分布と考えてよい。
例えば、上記の確率変数
が平均
、分散
に従うとする時、
もしくは、
和の期待値と分散は次のようになります。
についても同様に導出できます。
なんとなく、どんな母集団の分布でも標本数を増やすと正規分布になる、みたいな誤解がありそうですが、そんなことはなく、誤解を恐れずに言うと、標本の和や平均が正規分布に近づいていくということです。
標準正規分布に従う乱数の生成
ボックスミューラーの正規乱数生成については紹介しましたが、今回は上記の中心極限定理を使って生成したいと思います。
中心極限定理では、元の母集団はなんでもよいとのことですので、一様分布に従う確率変数を考えます。この一様分布の確率変数
を
個サンプリングすると、その平均
は
に従います。
次には一様分布
に従うので、その期待値と分散は次のようになります。
以上から、一様分布から個のサンプルを拾ってきて和を取った
は正規分布
に従います。
さらにこれを標準化します。実際の値をとすると、その和は
と表現できるので、標準化した値
は次のようになります。
標準化したので、は標準正規分布
に従います。では実装してみましょう。
#!/usr/bin/env perl use strict; use warnings; # perl random.pl > random_out.dat my $n = 12; my @random_numbers; for my $i ( 1..1000 ) { # 1000個の乱数を生成 my $sum_r = 0.0; for my $j ( 1..$n ) { $sum_r += rand(1); # 一様乱数の生成と足し合わせ } my $z = ($sum_r - $n/2)/sqrt($n/12); push @random_numbers, $z; } for my $k( @random_numbers ) { print $k."\n"; }
gnuplotを使ってヒストグラムを書きました。引用も追加しておきます。
set terminal png set output 'random_out.png' binwidth =0.5 bin(x,width)=width*floor(x/width)+width/2.0 plot [-4:4] 'random_out.dat' using (bin($1,binwidth)):(1.0) smooth freq with boxes title 'random\_out.dat'

それっぽく生成されています。
ちなみに、今回はを12として、1000個の正規乱数を生成しています。実は
とすると、
になるので、式が簡単になり、平方根の計算は入りません。コードは簡略化していませんが。
変数変換による正規分布 に従う乱数の生成
に従う乱数の生成
標準正規分布の乱数を作りましたが、次に
のような一般的な正規分布を作ります。
と言っても非常に簡単です。変数変換を施して生成します。生成したい平均、分散
の正規乱数を
、標準正規分布に従う変数を
とします。
上記のを生成して、
を乗じて、
を足し込めば完成です。さて実装です。
#!/usr/bin/env perl use strict; use warnings; # perl random_g.pl > random_out_g.dat my $n = 12; my $mu = 10.0; my $sigma2 = 5.0; my $sigma = sqrt($sigma2); my @random_numbers; for my $i ( 1..1000 ) { # 1000個の乱数を生成 my $sum_r = 0.0; for my $j ( 1..$n ) { $sum_r += rand(1); # 一様乱数の生成と足し合わせ } my $z = ($sum_r - $n/2)/sqrt($n/12); my $x = $mu + $sigma * $z; push @random_numbers, $x; } for my $k( @random_numbers ) { print $k."\n"; }
set terminal png set output 'random_out.png' binwidth =0.5 bin(x,width)=width*floor(x/width)+width/2.0 plot [0:20] 'random_out_g.dat' using (bin($1,binwidth)):(1.0) smooth freq with boxes title 'random\_out\_g.dat'

対数正規分布(その2)
中央値

参考
対数正規分布の前の記事は以下。
nishiru3.hatenablog.com
すごろく(第4回Perl入学式@東京)
Perl入学式
2019年7月13日に東京で第4回のPerl入学式が開催されました。
参加者の皆様、講師の@sironekotoro さん、サポーターの皆さんお疲れ様でした。
私はサポーターで参加させてもらいました。
内容
これまでのカリキュラムを多少変えて、第4回はひたすらリファレンスを学びます。
参加者の皆さんの中には、????という方も多かったと思いますが、復習問題を解くなどして、理解していただければなと。
すごろく
例のごとく、終了後のピザ会で@xtetsuji さんに出してもらったお題を当日20分くらいで解いてみました。
問題
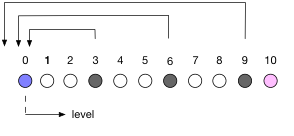
- 0から10までのマスがあり、0からスタートし、10に行けばゴールするすごろくがあります。
- 進む距離は1〜6の細工されていないサイコロで決めます。
- ただし、3、6、9のマスに止まった場合、スタートの0に戻されます。
- さて、平均的にサイコロを何回振ればゴールできるでしょうか?
ポイント
サイコロの確率分布
サイコロの1回の試行で出る目の確率分布は離散一様分布になります。
nishiru3.hatenablog.com
乱数の生成
Perlで乱数を生成する事が必要になります。
条件分岐
3、6、9でスタート地点に戻るという条件をif文で再現しています。
期待値の算出
平均的に何回か?という事なので、期待値の算出になります。最終行が期待値になります。
コード
#/usr/bin/env perl use strict; use warnings; use List::Util qw/sum/; # levelが10に達するまでにサイコロを振った回数 my @number_of_trials; for my $i (1..1000000) { # スタート地点は0 my $level=0; # サイコロを振った数を0にする。 my $number_of_trial = 0; # 1回ゴールするまでの繰り返し。 while(1) { # 一様乱数(1 ~ 6) my $number_of_dice = int(rand(6)) + 1; # サイコロを振った数を一つ増やす $number_of_trial++; # サイコロの出た目だけ進める。 $level = $level + $number_of_dice; # levelが3,6,9になったらスタート地点に戻す。 if( $level == 3 || $level == 6 || $level == 9 ) { $level = 0; } # levelが10に達したらゴール if( $level >= 10 ) { # ゴールするのにサイコロを振った回数を配列に記録 push @number_of_trials, $number_of_trial; # ループを抜ける last; } } } # ゴールするのにサイコロを振る回数の期待値 print sum(@number_of_trials)/scalar(@number_of_trials)."\n";
Vimの自動に作られるファイルを作らない
自動で作られるファイル
- .swp
- ~
- .un~
.swapは変更前のファイル。変更後はファイルは削除される。
~は変更後に作られる変更前ファイル。ファイルは削除されない。
.un~はundo情報。
.vimrcの設定
- set noswapfile
- set nobackup
- set noundofile








