nishiru3の日記

備忘録です。ネットのゴミ。

二項分布

確率 統計 二項分布

確率関数

定義は次のとおりである。
f(x) = {}_n C_x p^x (1-p)^{n-x}
確率変数X_1,X_2,・・・,X_nがベルヌーイ分布に従うとすると、X_1+X_2+・・・+X_nは二項分布に従う。
期待値および分散はベルヌーイ分布のn倍として覚えておくと便利。二項分布は、Bin(n,p)と表現する場合もある。

モーメント母関数f:id:nishiru3:20180611234724p:plain

モーメント母関数は次のとおりである。式の整理については、後述する二項定理
(a+b)^n = \sum^{n}_{k=0} {}_n C_k a^k b^{n-k}を使う。

f:id:nishiru3:20180611142515p:plain

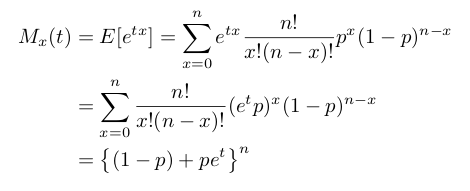
期待値

定義は次のとおりである。
E[X]=np

導出は次のとおりである。
P(X=x_k) = p_kとすると、
f:id:nishiru3:20180611142824p:plain
二項定理を使って変形している。

分散

定義は次のとおりである。
V[X]=np(1-p)

導出は次のとおりである。なお、E[X(X-1)]を求めてから、分散V[X]を求める。

f:id:nishiru3:20180611234724p:plain

f:id:nishiru3:20180611234918p:plain

その他

上記導出に用いた二項定理は次のとおり。

f:id:nishiru3:20180611235127p:plain

モーメント母関数を用いた期待値E[X]と分散V[X]の導出は次のとおり。

f:id:nishiru3:20180611235332p:plain

f:id:nishiru3:20180611235433p:plain

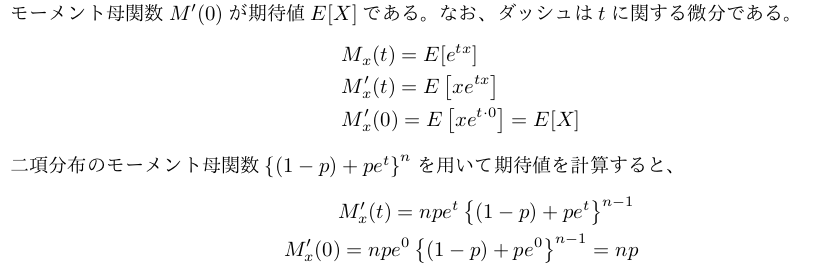
あまり厳密じゃない事に注意。

参考文献

数理統計学 (数学シリーズ)

数理統計学 (数学シリーズ)

数理統計学―基礎から学ぶデータ解析

数理統計学―基礎から学ぶデータ解析